cf932E. Team Work(第二类斯特灵数 组合数)

题意

题目链接

sol

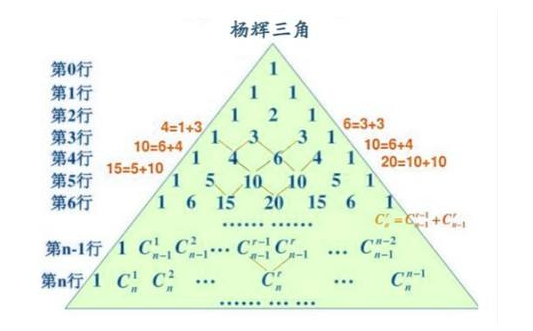
首先要知道第二类斯特灵数的一个性质

$$m^n = \sum_{i = 0}^m c_{n}^i s(n, i) i!$$

证明可以考虑组合意义：$m^n$是把$n$个不同的球放到$m$个不同的盒子里的方案数

然后用这个式子展开$i^k$，把组合数展开，会得到这样一个式子

$$\sum_{i=1}^n\frac{n!}{(n-i)!}\sum_{j=0}^i\frac{s(k,j)}{(i-j)!}$$

发现不是很好搞，但是考虑到当$j > k$时$s(k, j) = 0$，于是可以先枚举$s(k, j)$的贡献

$\sum_{j = 0}^n s(k, j) \sum_{i = 1}^n \frac{n!}{(n - i)!} \frac{1}{(i - j)!}$

把后面构造成组合数的形式

最终会得到

$$\sum_{j=0}^{k}s(k,j)\frac{n!}{(n-j)!}2^{n-j}$$

注意这里的阶乘是不能直接推的，可以维护化简之后的结果。

然后就做完了。

经验：

看到$i^k$想一想第二类斯特灵数

循环复杂度过高时考虑更换枚举顺序

看到分子分母中有阶乘时尝试构造组合数

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5001, mod = 1e9 + 7, inv2 = 500000004;
inline int read() {
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int n, k, s[maxn][maxn];
int fastpow(int a, int p) {
    int base = 1;
    while(p) {
        if(p & 1) base = 1ll * base * a % mod;
        a = 1ll * a * a % mod; p >>= 1;
    }
    return base;
}
int main() {
    s[0][0] = 1;
    cin >> n >> k;
    for(int i = 1; i <= k; i++)
        for(int j = 1; j <= k; j++)
            s[i][j] = (s[i - 1][j - 1] + 1ll * s[i - 1][j] * j % mod) % mod;
    int ans = 0, nv = 1, po2 = fastpow(2, n);
    for(int i = 0; i <= min(k, n); po2 = 1ll * po2 * inv2 % mod, nv = 1ll * nv * (n - i) % mod, i++)
        (ans += (1ll * s[k][i] * nv % mod * po2 % mod)) %= mod;
    cout << ans % mod;
    return 0;
}